当前位置:首页 >
高等数学(工本)(00023) > 正文内容
设函数u(x,y)=arctan(y/x),则du∣(3,4)=____.
设函数u(x,y)=arctan(y/x),则du∣(3,4)=____.
-(4/25)dx+(3/25)dy. 解析:∂u/∂x=1/[1+(y/x)2]•[-(y/ x2)]= -[y/(x2+y2)] ∂u/∂y=1/[1+(y/x)2]•(1/x)=x/(x2+y2) 所以∂u/∂x∣(3,4)=-[4/(32+42)]=-(4/25), ∂u/∂y∣(3,4)=3/25, 故 du∣(3,4)=∂u/∂x∣(3,4)dx+∂u/∂y∣(3,4)dy=-(4/25)dx+(3/25)dy.

扫描二维码免费使用微信小程序搜题/刷题/查看解析。
版权声明:本文由翰林刷题小程序授权发布,如需转载请注明出处。

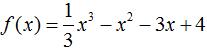 的极值.
的极值.