某公司利用两种原料A、B生产甲、乙两种产品（吨），单位产品所需的原料数、原料限量及单位产品所获利润如题40表。企业日标是追求利润的最大化，试写出该线性规划问题的数学模型，并用图解法求出最优解和最大利润。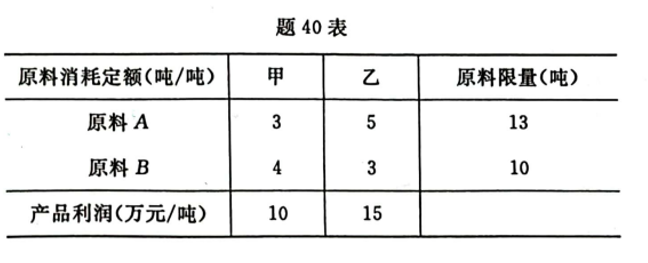

某公司利用两种原料A、B生产甲、乙两种产品（吨），单位产品所需的原料数、原料限量及单位产品所获利润如题40表。企业日标是追求利润的最大化，试写出该线性规划问题的数学模型，并用图解法求出最优解和最大利润。

设生产甲产品 X 吨,乙产品Y 吨,利润是S,线性规划模型如下:
目标函数,求利润S 的最大值:
S=10X+15Y
约束条件:
3X+5Y≤13
4X+3Y≤10
X,Y≥0

答40图
由 答40图可知:
最优解是 X=1,Y=2,最大利润是 maxS=40(万元)。