设三阶矩阵A=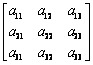的行列式不等于0，证明： 高老师2年前 (2024-03-26)线性代数（经管类）(04184)10

设三阶矩阵A=的行列式不等于0，证明：线性无关．

构造齐次线性方程组Ax＝0，即（，，）＝0，x1+ x2+ x3＝0， 由已知A的行列式不等于0，根据克莱默法则，方程组有惟一零解，即当且仅当x1＝x2＝x3＝0时， x1+ x2+ x3＝0 成了，所以向量组，，线性无关