设3元线性方程组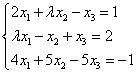,（1）确定当λ取何值时，方程组有惟一解、无解、有无穷多解？（2）当方程组有无穷多解时，求出该方程组的通解（要求用其一个特解和导出组的基础解系表示）

设3元线性方程组,（1）确定当λ取何值时，方程组有惟一解、无解、有无穷多解？（2）当方程组有无穷多解时，求出该方程组的通解（要求用其一个特解和导出组的基础解系表示）

取系数行列式 D＝，解得，，根据克莱默法则，且时，方程组有惟一解；当＝1时，方程组的增广阵为 此时，方程组有无穷多解，其通解为 x＝，其中为任意常数；当时，方程组的增广矩阵为 此时，方程组无解。总之，（1）当且时，即，方程组有惟一解，当＝1时，方程组一无穷多解，当时，方程组无解；（2）当＝1时，方程组的通解为x＝，其中为任意常数。