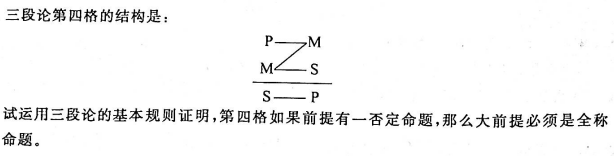
证明(反证法):假设前提中有一否定命题,且大前提并不是全称命题。如果前提有一否定命题,且大前提不是全称命题,若大前提否定,根据第4格形式可知,大前提中大项不周延,中项周延。根据规则7,前提中有一特称命题,则结论必须是特称命题。根据规则3在前提中不周延的项在结论中也不得周延,可知,结论的谓项不周延,故结论为I判断(即肯定判断)。根据规则5,前提中有一否定,结论必定否定,可知,上述推理与规则矛盾。所以设不成立,故前提中有一否定命题,则大前提必须是全称命题。